Do adversarial defenses improve the robustness of DNNs?

Code: https://github.com/LEGO999/AD_robustness

Deep Neural Networks (DNNs) are known to be prone to adversarial attacks. Adversarial attacks manipulate predictions of DNNs via adding crafted perturbations, as shown in Fig.1.

^{Fig.1 An adversarial example generated by FGSM (source: Goodfellow et al., 2014)}

In essence, adversarial attacks optimize the following objective function to maximize the prediction error:

$$\mathbb{E}_{x, y}[\max_{\delta\in\Delta}\text{Loss} (f_{\theta}(x+\delta),y)]$$

Adversarial defenses could be solutions for adversarial attacks. They improve the robustness of DNNs against the most confusing samples (adversarial samples). This article serves to investigate whether adversarial defenses also improve other robustness of DNNs, which are:

• uncertainty calibration for in-distribution input
• out-of-distribution detection
• robustness under distributional shift
• rotational invariance

Setup

Defense Methods

The classical PGD adversarial training (Madry et al., 2017) and the state-of-the-art DDPM data augmentation (Rebuffi et al., 2021) are chosen in our experiments. The latter was first in the ranking of the RobustBench leaderboard when this investigation was conducted.

Evaluation

Adversarial Robustness

This section serves to verify our models and demonstrate the effectiveness of adversarial defenses. An untargeted PGD attack (Madry et al., 2017) with $\text{L}_{\inf}=8/255$ is used to confirm whether trained models are adversarial robust. The number of iterations is set to seven. The metric of adversarial robustness is robust accuracy ($\uparrow$).

Uncertainty Calibration for In-distribution Input

Modern DNNs are often miscalibrated (overconfident). To be specific, DNNs predict higher likelihood than actual accuracy. Expected Calibrated Error (ECE) ($\downarrow$) was proposed to measure the deviation of likelihood from accuracy. It could be calculated using the following equation:

$$\text{ECE} = \sum_{m=1}^{M}\frac{\left|n_m\right|}{B}\left|\text{acc}_m-\text{conf}_m\right|$$

where $M$ is the number of bins, $n_m$ is the number of samples falling into the bin $m$, $\text{acc}_m$ and $\text{conf}_m$ are the mean accuracy and mean confidence (top-1 predictive likelihood) of the bin $m$ respectively. We adopt the static binning scheme with 100 bins in our experiments. As stated in Patel et al., 2020, ECE estimation with 100 bins is insensitive to the choice of a particular binning scheme .

Out-of-distribution Detection

DNNs are trained on a training set and requested to predict on both in-distribution (label0) and out-of-distribution test sets (label 1). A robust classifier should well distinguish between two test sets. In this article, Area Under Receiver Characteristic Curve (AUROC) ($\uparrow$) is taken as the metric for out-of-distribution detection. The entropy of predictions is selected as the threshold in the AUROC.

Robustness under Distributional Shift

The CIFAR-C dataset (hendrycks et al., 2019) incorporates 19 kinds of common corruptions with five different severities in the real-world environment to the CIFAR test set. With evaluation on corrupted data, we could examine generalization (accuracy) ($\uparrow$) and model calibration (ECE) ($\downarrow$) of DNNs under distributional shift. An example of corrupted data is shown in Fig.2.

^{Fig.2 An example of corrupted data (source: hendrycks et al., 2019)}

The complete list of corruptions is attached:

Rotation Invariance

DNNs trained by adversarial defenses are assessed with rotated input. We are curious whether adversarial defense could generate rotation invariant predictions in this circumstance. As shown in Fig.3, the angles of rotation range from 0 degree to 180 degrees with the step size of 15 degrees. The generalizability is measured by accuracy ($\uparrow$).

^{Fig.3 Rotated CIFAR-10 images}

Datasets and Models

Constrained by the computational resources, we select the pre-trained models on CIFAR-10. The vanilla and PGD defense model come from Pytorch-Adversarial-Training-CIFAR. The DDPM defense model comes from their official repository.
The vanilla and PGD defense models use ResNet-18, while the DDPM model uses ResNet-18 with pre-activation. Though the architectures are slightly different, it should not have significant impact on our conclusions.
For out-of-distribution detection, we use Street View House Number (SVHN) and Kuzushiji-MNIST (KMNIST) as counterparts of the CIFAR-10 test set.

^{Fig.4 Examples of SVHN (four images on the left) and KMNIST(four images on the right)}

Naturally, CIFAR-10-C is selected as the corrupted dataset for distributional shift.

Experiments

Adversarial Robustness

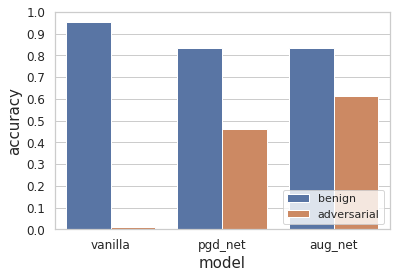
^{Fig.5 Benign accuracy and robust accuracy of the vanilla model (vanilla), the PGD defense model (pgd_net) and the DDPM augmented model (aug_net)}

From Fig.5, for the benign input, the vanilla model outperforms pgd_net by a large margin (over 10%). pgd_net and aug_net have similar performance. When we switch to adversarial input, the vanilla model is completely shattered and fails to classify most samples correctly. aug_net demonstrates the state-of-the-art adversarial resistance and achieves the best robust accuracy among three methods, about 61%.
pgd_net is the first runner-up. The big gap (about 15%) of robust accuracy between the pgd_net and aug_net shows the recent advances in adversarial machine learning.
This section demonstrates the vulnerability of the vanilla model and verifies the correctness of our setup.

Uncertainty Calibration for In-distribution Input

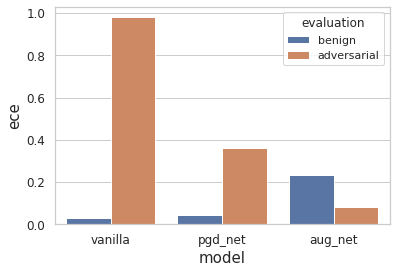
^{Fig.6 Benign ECE and robust ECE under untargeted PGD attack of vanilla, pgd_net and aug_net}

From Fig.6, in the benign setup, despite regularization from PGD training and DDPM augmentation, both of them fail to mitigate the miscalibration of DNNs. Chun et al., 2020 has a similar observation for PGD training. Unfortunately, they failed to disentangle the influence of PGD training as label smoothing is enabled in their setup. aug_net suffers more severely from miscalibration than pgd_net.
In the adversarial setup, it is not surprising that the aug_net has the lowest ECE error, while vanilla carries the highest ECE error. This corresponds to their robust accuracy. Intuitively, a PGD attack aims to maximize the prediction error whilst adversarial defenses could hinder such kind of sabotage.

Out-of-distribution Detection

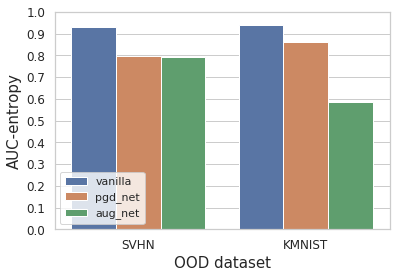
^{Fig.7 AUC-entropy of the vanilla, pgd_net and aug_net}

From Fig.7, when the out-of-distribution input comes from SVHN, pgd_net and aug_net perform worse than the vanilla baseline. aug_net is marginally worse than pgd_net. When outliers come from KMNIST, both adversarial defense methods fail to detect them better than vanilla. aug_net’s AUC drops significantly to approximately 0.6 and is close to random guessing (0.5). This part of the experiments suggests that adversarial defense will impart DNNs’ capability to detect out-of-distribution samples.

Robustness Under Distributional Shift

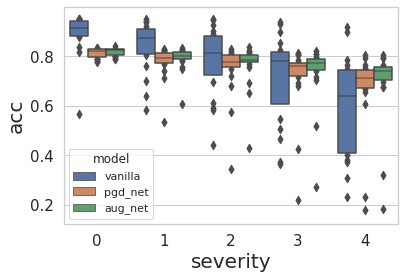
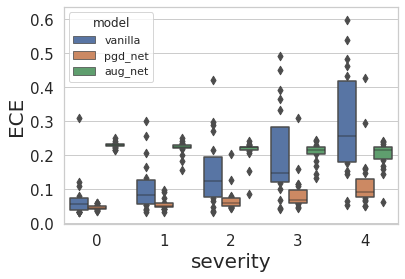
^{Fig.8 accuracy and ECE of vanilla, pgd_net and aug_net under different severities of corruptions}

All methods are evaluated on CIFAR-10-C for five severities. Talking about the accuracy, as shown in Fig.8, all methods are more or less affected by the corruptions. When the corruptions are mild (severity 0 and 1), vanilla is superior to pgd_net and aug_net. At higher severities, vanilla’s accuracy is scattering over the whole spectrum, indicating that vanilla is not robust under distributional shift. In contrast to vanilla, pgd_net and aug_net demonstrates more consistent generalization even at high severities. aug_net outperforms pgd_net marginally at all severities.

Speaking of ECE, pgd_net has the lowest ECE for all severities of corruptions. At low severities (i.e. 0, 1 and 2), vanilla is better calibrated than aug_net. At high severities, it’s hard to tell if vanilla or aug_net is more miscalibrated. But one thing is for sure, vanilla has larger interquartiles than aug_net as perturbation intensity increases.

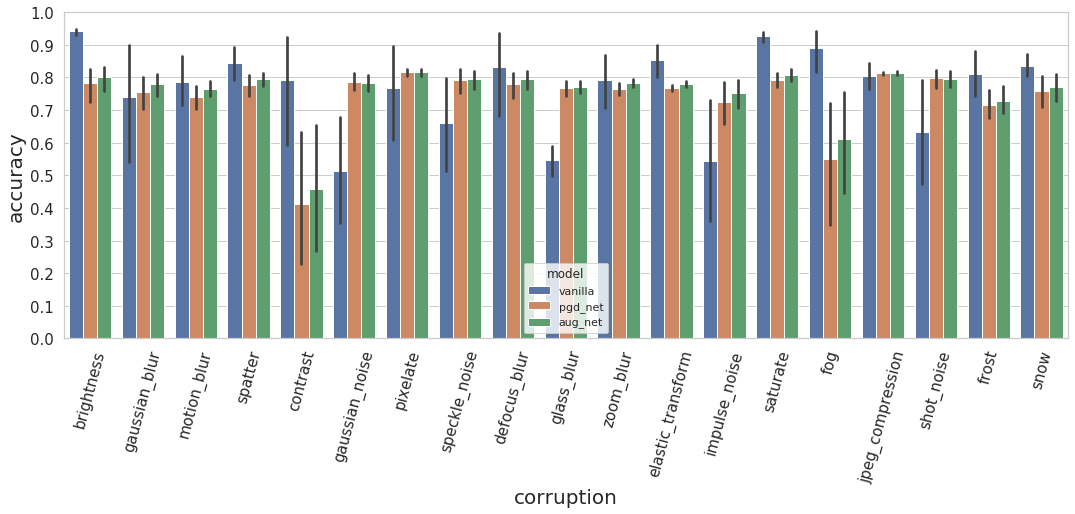
^{Fig.9 Accuracy of the vanilla, pgd_net and aug_net under distributional shift. The average of five severities and the standard deviation is shown.}

To investigate the sensitivity of methods to different corruptions, we group the result according to the type of corruptions. We plot the accuracy under different kinds of corruptions in Fig.9. In general, pgd_net and aug_net are similar in accuracy. aug_net is slightly better. In Tab.1, we summarize the situations, in which adversarial defenses are inferior (“deterioration”) and superior (“improvement”) to the vanilla model.

As shown in Tab.1, adversarial defenses enormously improve DNNs’ robustness against different kinds of noise (e.g., Gaussian and speckle) but also degenerates generalization under corruptions like weather (e.g., fog, frost)and illumination conditions (e.g., brightness, contrast). We conjecture that this can be explained by the impaired generalizability of adversarial defenses with benign input.

Rotational Invariance

Human can easily recognize the rotated objects without special training. We expect our DNNs to make rotation-invariant decision, though there is no explicit rotational data augmentation in training of these models. When DNNs are unlikely to give correct predictions, we expect them to know when they don’t know. Do adversarial defenses help improve these?

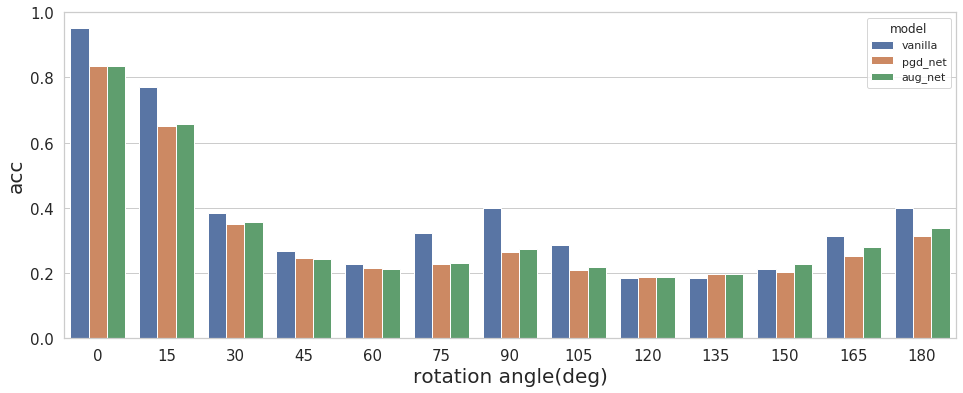
^{Fig.10 Accuracy of vanilla, pgd_net and aug_net with rotated input}

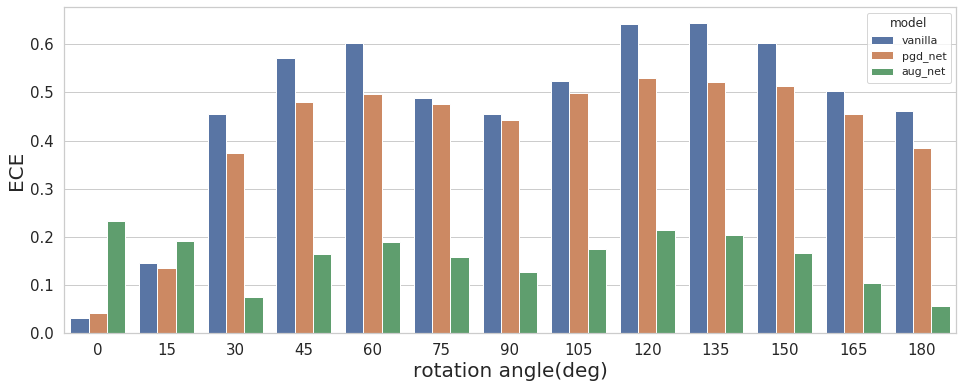
^{Fig.11 ECE of vanilla, pgd_net and aug_net with rotated input}

As shown in Fig.10, the ranking of accuracy is almost the same across different angles. vanilla is the champion, and aug_net is the first runner-up. pgd_net performs slightly worse than aug_net and takes the last place. This result is consistent with the result of benign input in the section of adversarial robust. It also shows that adversarial defenses do not help improve the generalization of DNNs with rotated input. Nevertheless, adversarial defenses do improve the uncertainty calibration of DNNs. As we can see from Fig.11, pgd_net and aug_net has larger ECE than vanilla when there is no rotation (0 degree). With increasing rotation angles, the predictions of the vanilla model become more miscalibrated. pgd_net also suffers from miscalibration with increasing rotation but still works slightly better than vanilla. Unlike vanilla and pgd_net, aug_net is consistently well-calibrated when rotation is larger than 30 degrees. aug_net is rather robust with a large rotation in input.

Conclusion

In this article, we systematically evaluate the robustness of adversarial defense models in terms of adversarial robustness, uncertainty calibration for in-distribution input, out-of-distribution detection, robustness under distributional shift and rotational invariance.
In conclusion, adversarial defenses succeed in providing better generalization and uncertainty calibration with adversarial in-distribution input. Unfortunately, it is not the case with benign in-distribution input. Tsipras et al., 2018 claimed that adversarial defenses are trade-offs between robustness and standard accuracy. They also attributed the robustness to different learned feature representations. Improving the generalization of adversarial defense with benign input is still an open question.
Another drawback of adversarial defenses could be, they fail to detect out-of-distribution samples.
As for distributional shift, adversarial defenses deteriorate DNNs’ performance given the weather and illumination variations. However, it also puts up strong resistance to different kinds of noises. Serval certifiable adversarial defense methods (e.g., Li et al., 2018 and Cohen et al., 2019) try to linked to adversarial robustness to noise. Unfortunately, certifying is quite resource-consuming (several hours to certify a CIFAR-10 test set). The theory to explain adversarial robustness is still not fully explored and is worth digging in.
Adversarial defenses do not facilitate generalization with rotated input. However, adversarial defenses improve uncertainty calibration of DNNs while the vanilla model still suffers from miscalibration given rotated input.